2018年 11月 1日
前回 HSPの rnd関数では 32768までの乱数しかでないので、どうやってそれ以上の乱数を出すかやりました、その続きです。
実数(小数)での乱数発生を試してみたら、こちらの方が分かりやすく簡単だったので、それを使う事にした。
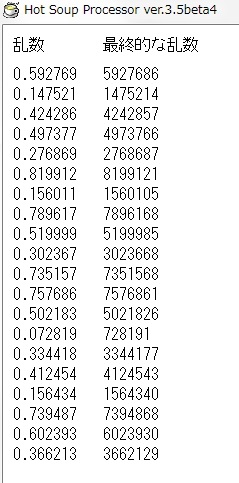
#include "hspda.as" ; 実数乱数用 rndf_ini ; 乱数の初期化 randomize pos 10,10 : mes "乱数" pos 100,10 : mes "最終的な乱数" r=10000000 ; 出したい乱数 repeat 20 rndf_get f ; 0~1の乱数、0.000001ケタ pos 10,cnt*20+40 : mes f n=int(double(r)*f) ; 出したい乱数に%を掛ける pos 100,cnt*20+40 : mes n loop
#include “hspda.as” .asファイルは外部 DLLという訳では無いので HSP Dishでもたぶん問題ない。
実数(小数点)の乱数とは 0~1の、つまり 0.000001~1.000000までの乱数で、100%が 1.0となる。
この数に求めたい乱数の数を掛ければよい。
つまり前回の整数乱数だと最大で 1/32768の精度だったけど、これだと最大で 1/1000000(百万)の精度になる(はずなんだけど、どういう訳かそれ以上のケタでも 1単位で乱数が出るような・・・)
つまり 1000000以下の数であれば 1ずつの乱数を出せると言う訳だ。
関数化(擬似命令化)してみる
#include "hspmath.as" ; 計算(round用) #include "hspda.as" ; 実数乱数用 rndf_ini ; 乱数の初期化 gosub *main #defcfunc rnb int rnbn ; 大きい数の乱数 rndf_get rnbf ; 0~1の実数乱数、0.000001ケタ rnbg=int(round(double(rnbn)*rnbf)) ; 出したい乱数に%を掛ける return rnbg *main r=2147483648-1 ; 2147483648 ; 最大数 repeat 20 n=rnb(r) mes n loop
よし、ではランブ関数と名づけよう(適当)
冗談はさておき、HSPで扱える数の最大が 2147483648なのだが、その数でやると値が -になるので、-1の 2147483647がこの方法で求められる最大乱数という事にたぶんなるだろう(確証は無い)
