1MAP_STG 当たり判定の研究編

　そういえば去年もたしかこれはゴールデンウィーク企画だった。
　
　
　今回の本丸は線と円の当たり判定なのだが、まずはおさらいと刷新をかねて、矩形と矩形、円と円などの当たり判定を求めるための勉強から始めたいと思う。

　今回の師匠はこちら

【初級プログラミング】STG・ACTゲーム 当たり判定【ゆっくり++】

　ニコニコ動画さんです。

　
　
1、矩形と矩形

　それではまず矩形と矩形、四角同士の当たり判定をやりますけど、今回は中心座標から半分の大きさの距離を計る方法をやってみます。

　jx,jy = 自機の座標
　ex,ey = 敵の座標
　jo = 自機の大きさ
　eo = 敵の大きさ
　jh = 自機の大きさの半径
　eh = 敵の大きさの半径
　
　

　
　
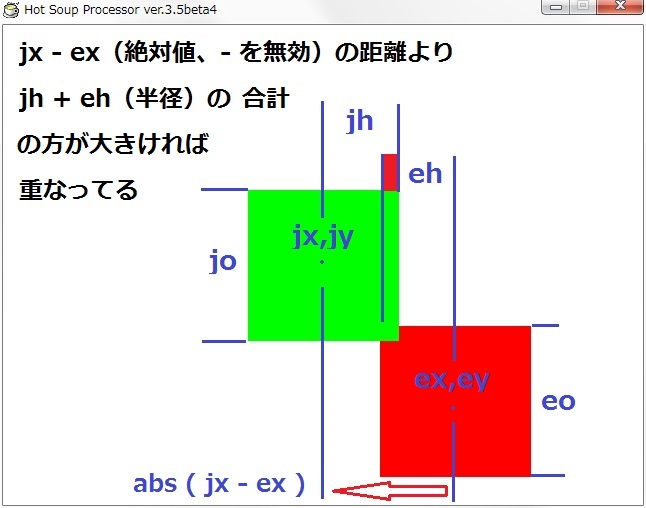
　ex – jx の差の絶対値（つまり負 – の数が全て正の数 + になります、例えば -10だと 10になります）を求めます、絶対値という事は jx – exでも同じ値になります。

　絶対値を求める命令は absです。

　jh + eh 自機と敵の半径の合計を求めます。

　自機と敵の中心の距離より、半径の大きさの合計が大きければ重なってる事になります。

　y（横軸）で判定した後、重なっていれば x(縦軸)で判定します。

　なぜ yが先なのかは、画面の長さやゲーム内容的に y軸がかぶる事の方が少ないからでしょう。

　という事は、たぶん横スクロールタイプなら x軸からしたら良いんだと思います。

; 当たり判定
　f=0 ; 当たり判定フラグ
　if abs(jy-ey)<=(jh+eh) {
　if abs(jx-ex)<=(jh+eh) : f=1
　}

　今度は円と円の当たり判定です。

　同じように自機と敵の中心点の距離より、自機と敵の半径合計が大きければ重なっています。
　
　

　
　
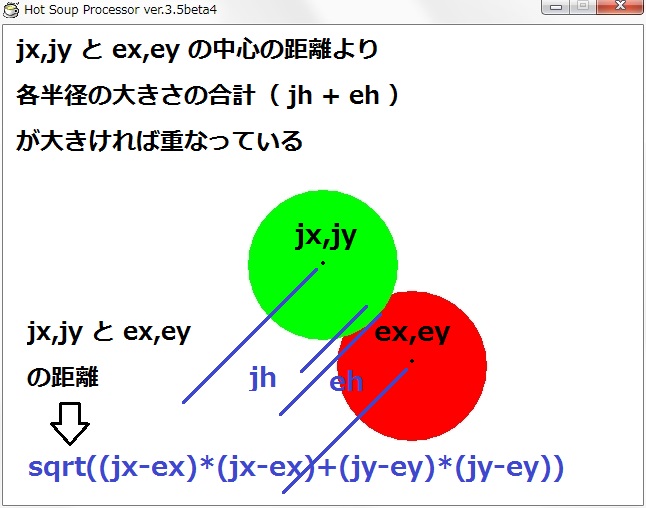
　2点間の距離を求める式は

　sqrt((ex-jx)*(ex-jx)+(ey-jy)*(ey-jy))　ですが

　sqrtは平方根で √（ルート）の命令です。

　hx = ex – jx
　hy = ey – jy

　とすると

　sqrt((hx)*(hx)+(hy)*(hy))

　と短縮できます。
　
　
　ho = jh+eh　自機と敵の半径の合計として、

　当たり判定の式は

　if sqrt((hx)*(hx)+(hy)*(hy))<=ho : f=1

　となりますが、ルートの分、両端をそれぞれもう一度同じ式でかけて（両辺を 2乗する）

　if (hx*hx)+(hy*hy)<=(ho*ho) : f=1

　という式で良いそうです。

　sqrtの命令が遅いらしいので、これだと高速にできるという事だそうです。

　動画だとさらに 1と 2をミックスして、高速化技が紹介されています。

　要するに矩形判定をしてから円判定をします。

　f=0 ; 当たり判定フラグ
　if abs(ey-jy)<=(jh+eh) {
　if abs(ex-jx)<=(jh+eh) {
　　if (hx*hx)+(hy*hy)<=(ho*ho) : f=1
　}
　}

　HSPならさしずめこうでしょう。

　f=0 ; 当たり判定フラグ
　repeat j
　　if abs(ey-jy)>(jh+eh) : break
　　if abs(ex-jx)>(jh+eh) : break
　　if (hx*hx)+(hy*hy)<=(ho*ho) : f=1
　loop
　
　
　
4、線と円との当たり判定

　ここからが今回の本丸です。

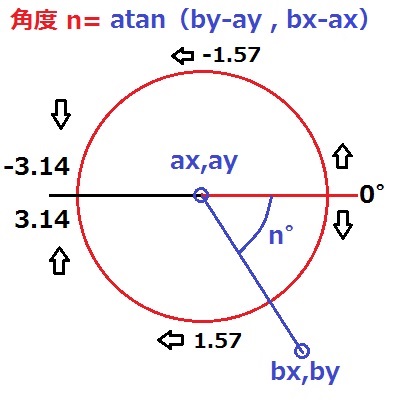
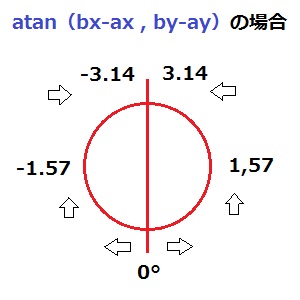
　まず前の記事で角度を求める atan(by-ay,bx-ax) の使い方、つまり atan の使い方が間違っていた。

　改めて HSPのヘルプ説明書を見ると atan(y,x) が正解で、これだと右側を角度 0にしてくれる。

　前回は atan(x,y) と xと yを逆に記述していたために、上が確度 0でおかしかった。

　始点を ax,ay 終点を bx,by とすると、正しい記述は atan(by-ay,bx-ax) となる。
　
　
　これだと以下の図のようになり、たぶんこれが正規だと思う。

　
　
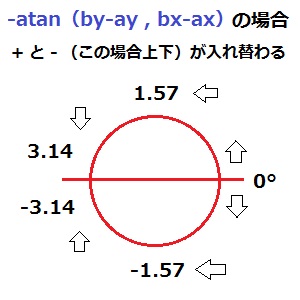
　ちなみに前回の記述 atan(ax-bx,ay-by)だとこうなる。

　
　
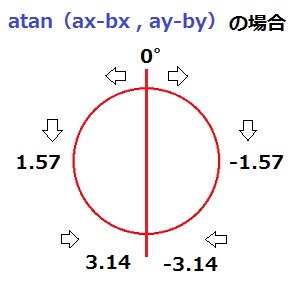
　atan(ay-by,ax-bx) の場合

　
　
　atan(bx-ax,by-ay) の場合

　
　
　まとめるとこうなる。

　　atan(by-ay,bx-ax) 右、正規
　　atan(bx-ax,by-ay) 下
　　atan(ax-bx,ay-by) 上
　　atan(ay-by,ax-bx) 左
　
　
　ちなみに前回やったように、+ – の符号を変えると逆になる。

　
　
　以上、前回はきちんと把握してなかった atanの仕様でした。
　
　
　それでは線と円の当たり判定をやります。

　考え方は動画によると、まず線 ABが水平になる角度を求めて、円をその角度分回転移動します。

　線 ABが水平の位置なら、円の当たり判定は、単に円の中心点の y座標が、円の半径より小さければ当たっている事になります。

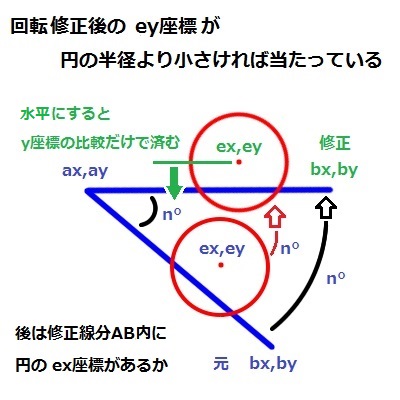
　後は線分 AB上の x座標内に、円の x座標があるかどうかです。
　
　
　それでは当たり判定をやってみましょう。

　今回、式の内容が分からず解いてる時間も無かったので、動画内の式をそのまま使い、説明は割愛します。

　やってる事は三角関数で弧円を描くのと同じ原理だと思います。
　
　
; 当たり判定

　f=0 ; 当たり判定フラグ

　rad=atan(by-ay,bx-ax) ; 線ABの角度

　abn=sqrt((bx-ax)*(bx-ax)+(by-ay)*(by-ay)) ; 線の長さ

　xn=ex-ax ; 円x-線始点ax
　yn=ey-ay ; 円y-線始点ay

　cosf=cos(-rad) ; 角度修正、水平に
　sinf=sin(-rad) ; 角度修正、水平に

　xf=cosf*xn-sinf*yn ; 水平位置に修正した円のx
　yf=sinf*xn+cosf*yn ; 水平位置に修正した円のy

　if abs(yf)<=eh and 0<=xf and xf<=abn : f=1 ; 当たり判定 　
　

　
　
　できました。

　
　
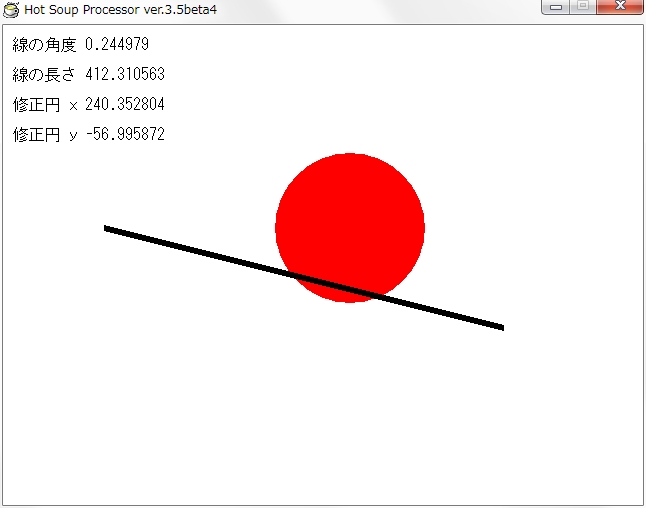
　でもこれだけだど問題があって、半径の分、両端に死角ができます。

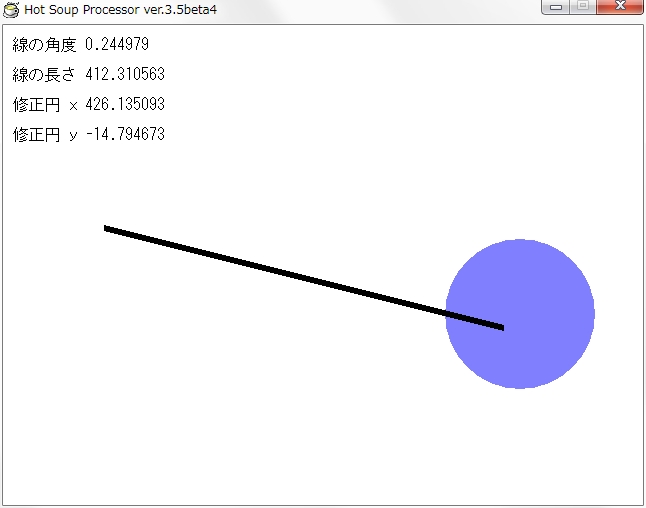
　そこで動画にもありますけど、A点 B点両端から円の半径内に円の中心があるか距離を測ります。

　
　
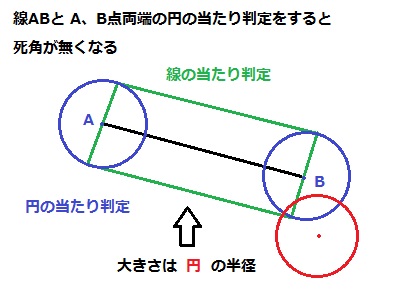
　if f=0 { ; 両端判定
　　if (ex-ax)*(ex-ax)+(ey-ay)*(ey-ay)<=(eh*eh) : f=1 ; a点と円の当たり判定
　　if (ex-bx)*(ex-bx)+(ey-by)*(ey-by)<=(eh*eh) : f=1 ; b点と円の当たり判定
　}

　これで両端の当たり判定もカバーできます。

　
　
　
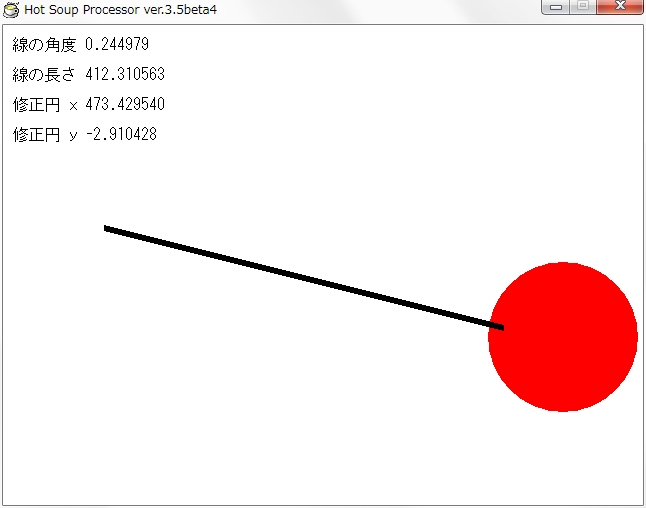
　今回は前半としてここまでにします。